
Generating asymptotically uniform distributions from Plinko boards.
Plinko is a game of chance, featuring a board, ball, and buckets. The board features a set of pegs positioned such that the ball may fall and bounce between them, going to the left or right of a given peg with predetermined probabilities. Buckets are positioned at the bottom of the board in a way that the ball must fall into one of them. The game is played by dropping the ball from the top of the board, and the player wins whatever prize is associated with the bucket the ball falls into.

Most variants of the game:
A few notable examples of this game in action:
To make analysis simpler, we'll constrain Plinko to only allow the player to drop the ball onto one starting peg, and furthermore, no walls will be present.
In any real-life Plinko board I have observed, the probability of going left at any peg is approximately .5 (and .5 for right by complement). This means the pegs may be thought of IID Bernoulli trials, inducing a Binomial distribution determining the final bucket landed in (by summing up the number of left/right falls). Frustratingly, Plinko is often referenced as a demonstration of the Central Limit Theorem (CLT). This is true, but it's disingenuous to imply such directness. The direct distribution is binomial(n=board depth,p=.5), which is asymptotically approximated by the Normal distribution through the CLT (as a linear combination of IID Bernoulli trials) at large n and n*p.
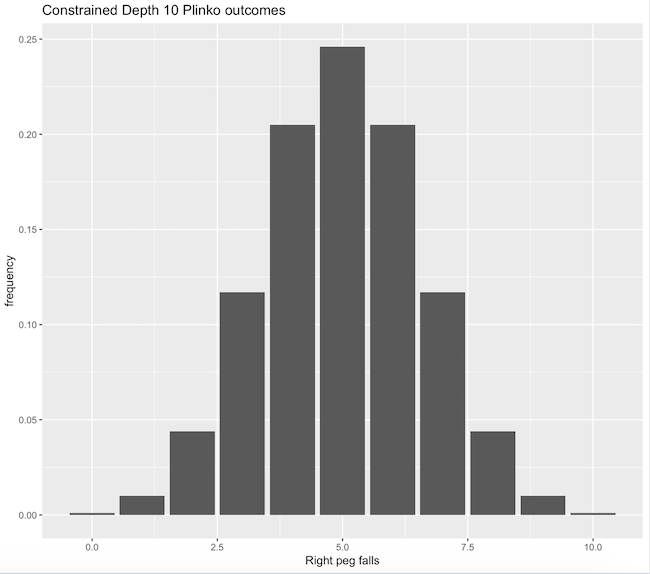
Here's the asymptotic break out of bucket outcomes for a constrained depth 10 Plinko board under 50/50 splits:
And the visual distribution:
Great! In the boring world, we have a binomial distribution. Can we construct Plinko boards that produce other distributions? Specifically, can we construct the uniform distribution for any depth Plinko board?
Some thoughts relevant to this problem:
The approach taken was brute force and numerical:
At this point, we have a system of equations! That is, an equation per bucket, with each equation equal to uniform density 1 / (1 + n). For example, a depth 2 board with 3 nodes has the following system, where x_i is the probability of falling left for the ith node, labelled 1...3 top to bottom, left to right:
x_1 * x_2 = 1 / 3
x_1 * (1-x_2) + (1 - x_1) * x_3 = 1 / 3
(1 - x_1) * (1 - x_3) = 1 / 3
In general, this system will be underdetermined. For a depth n board, there are n + 1 buckets, leading to n + 1 equations of n(n+1)/2 parameters. So, we prefer an optimization approach. I chose to define a loss function on the bucket outcomes B_i as: (1 / (n + 1) - B_i)^2, which is simply squared loss on the uniform density. Depending on the numerical optimization method used, other loss functions may be more ideal. With a loss function in hand, all that is left is to apply a gradient based optimizer. I had success with BFGS, constraining the state space to [0,1] (valid probabilities) for all parameters.
Solutions are rendered with right fall probabilities only; left fall probabilities are simply derived as the complement. Note that the solutions are rounded to two decimal places for clean rendering. To reproduce these results and graphics see uniform_plinko.py.
Using the above python code, this solution took around 10 seconds to compute.